金属丝的杨氏模量-金属丝的杨氏模量一般多大

大家好，今天小编关注到一个比较有意思的话题，就是关于金属丝的杨氏模量的问题，于是小编就整理了3个相关介绍金属丝的杨氏模量的解答，让我们一起看看吧。

钢丝杨氏模量的计算公式？

钢丝杨氏模量值e的公式：E=2.06e11Pa=206GPa。

钢材的弹性模量(e11表示10的11次方)它只与材料的化学成分有关，与温度有关。与其组织变化无关，与热处理状态无关。钢丝时不具有公称弹性模量的，然而在一规定载荷范围内可以测定钢丝绳的“近似的”弹性模量。它称为钢丝的实际弹性模量。

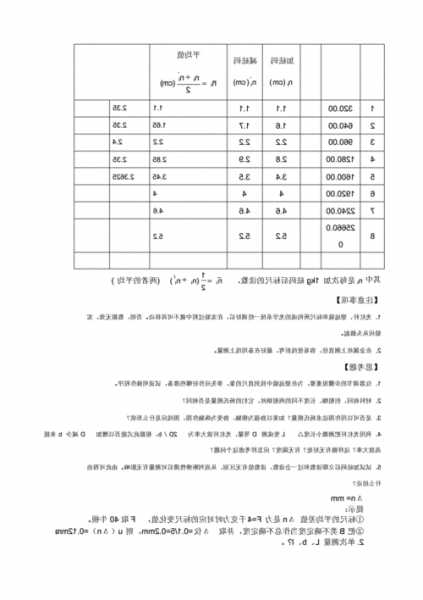
杨氏模量的逐差法公式：η＝W有/Wd。杨氏模量是描述固体材料抵抗形变能力的物理量。当一条长度为L、截面积为S的金属丝在力F作用下伸长ΔL时，F/S叫应力，其物理意义是金属丝单位截面积所受到的力；ΔL/L叫应变，其物理意义是金属丝单位长度所对应的伸长量

拉伸法测定金属丝的杨氏模量e为？

应力（σ）单位面积上所受到的力（F/S）。 应变（ε ）：是指在外力作用下的相对形变（相对伸长DL/L）它反映了物体形变的大小。 杨氏模数(Young's modulus )是材料力学中的名词，弹性材料承受正向应力时会产生正向应变，定义为正向应力与正向应变的比值。公式记为 E = σ / ε 其中，E 表示杨氏模数，σ 表示正向应力，ε 表示正向应变。 杨氏模量大 说明在 压缩或拉伸材料，材料的形变小。

拉伸法测量金属丝的杨氏模量逐差怎么求？

关于这个问题，杨氏模量的计算公式为：$E=\frac{F/A}{\Delta L/L}$，其中$F$为施加的拉力，$A$为金属丝的横截面积，$\Delta L$为金属丝伸长的长度，$L$为金属丝的原始长度。

拉伸法测量金属丝的杨氏模量逐差指的是，分别施加不同的拉力，测量相应的伸长长度，然后计算出每个拉力下的杨氏模量，最后计算相邻两个拉力下的杨氏模量的差值。

具体步骤如下：

1. 选择一根长度足够长的金属丝，并测量其直径，计算出其横截面积。

2. 在金属丝两端分别固定两个夹具，夹具间的距离即为金属丝的原始长度。

3. 施加第一个拉力，记录金属丝的伸长长度。

4. 计算第一个拉力下的杨氏模量：$E_1=\frac{F_1/A}{\Delta L_1/L}$。

5. 施加第二个拉力，记录金属丝的伸长长度。

6. 计算第二个拉力下的杨氏模量：$E_2=\frac{F_2/A}{\Delta L_2/L}$。

7. 计算第一个拉力和第二个拉力下的杨氏模量的差值：$\Delta E=E_2-E_1$。

8. 重复以上步骤，施加更多的拉力，计算出相邻两个拉力下的杨氏模量的差值。

9. 将所有的杨氏模量的差值求平均，即为金属丝的杨氏模量逐差。

拉伸法测量金属丝的杨氏模量逐差是通过计算材料在两个不同的应变下所施加的应力之差，再除以应变差计算得到的。
具体公式为 ΔE/Δε=(F₂-F₁)/(A0L(ε₂-ε₁))，其中ΔE表示变化的杨氏模量，Δε表示变化的应变，F₂和F₁分别表示在两个应变下施加的应力，A0表示材料的横截面积，L表示测试样品的初始长度，ε₂和ε₁分别表示两个应变的大小。
拉伸法测量杨氏模量是一种常见的材料力学性能测试方法，用于评估材料的刚度和弹性性。
除了金属丝，该方法还可用于测试其他材料，如聚合物、复合材料等。
在实际测试中，还需要考虑多种因素对测试结果的影响，如温度、湿度、测试速度等。

到此，以上就是小编对于金属丝的杨氏模量的问题就介绍到这了，希望介绍关于金属丝的杨氏模量的3点解答对大家有用。